Publisher: PMLR 2022
Author: 丁天骄, 德里克·林, 雷内·维达尔, 本杰明·海菲勒
摘要
将矩阵投影到双随机矩阵空间上的问题在机器学习中有几个应用。例如,在谱聚类中,从数据亲和矩阵形成归一化拉普拉斯矩阵与将其投影到双随机矩阵集上密切相关。但是,关于此投影为何改善聚类的分析有限。在本文中,我们提出了给定亲和矩阵的理论条件,在该条件下,其双随机投影是理想的亲和矩阵(即,它在簇之间没有假连接,并且在每个簇内连接良好)。我们还表明,投影亲和矩阵理想的必要和充分条件简化为输入亲和力上的一组条件,这些条件沿每个类簇分解。此外,在子空间聚类问题中,每个类都由线性子空间定义,我们在底层子空间上提供了几何条件,这些条件通过问题的连续版本保证了正确的聚类。这使我们能够从理论上解释最近提出的双随机子空间聚类方法的显着性能。
1. 简介
谱聚类
尽管谱聚类的步骤简单且固定,但是其中几个实施细节却能相当大地影响谱聚类的性能。例如,affinity矩阵的定义似乎是人们需要考虑的。 但是,一个受到较少关注但可能对性能产生重大影响的细节是如何对affinity矩阵进行normalization。 实际上,两种最受欢迎的光谱聚类方法,Ratio cut和Normalized cut 使用了两个不同的normalization,这些normalization是两种不同的聚类的连续放松目标。 Zass&Shashua(2006)提供了另一种观点,他认为这些用于使亲和力矩阵归一化的方法与将亲和力投射到双随机矩阵的空间密切相关,方法之间的差异在于投影中什么距离被最小化了。
Zass and Shashua. Doubly stochastic normalization for spectral clustering. Advances in neural information processing systems, 19, 2006.
回想一下理想的亲和力矩阵满足两个属性:1) 连通性,即簇内点之间的非零元素形成一个完全连接的图; 2) 没有错误连接,即没有两个不同类簇之间的连接。
例如,子空间聚类问题考虑(近似)支持低维线性子空间并集的数据,其中每个线性子空间定义一个类。 子空间聚类通过将每个数据点表示为所有其他数据点的线性组合并在系数矩阵上强制执行稀疏或低秩属性来计算affinity矩阵。 即使affinity矩阵违反了没有错误连接的条件,适当的归一化仍然可以产生理想的affinity。 事实上,已经提出了大量的方法来标准化亲和矩阵,超出 NCut 或 RatioCuts 固有的标准Normalizaiton,以至有人认为,许多提议的聚类算法所声称的大部分好处实际上可以在很大程度上归因于临时affinity标准化。 为了寻求一种更有原则的affinity标准化方法,Lim 等人 (2020) 通过将亲和力矩阵投影到
ℓ
2
\ell_2
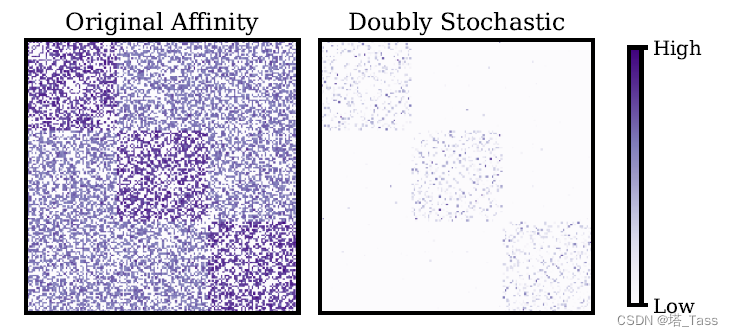
ℓ2距离下的双随机矩阵空间来对亲和力矩阵进行标准化,并在大量数据集上达到了SOTA性能 。 这在图 1 中进行了说明,它表明在
ℓ
2
\ell_2
ℓ2 度量下投影到双随机矩阵后,具有大量错误连接的非常嘈杂的亲和力矩阵变得近乎理想。
贡献
在这项工作中,我们给出了双重随机投影的严格理论分析。首先,我们证明了输入affinity的一个充要条件:即使原始affinity矩阵可能包含大量的错误连接,双重随机投影后的affinity也不存在假连接。虽然最优性条件将来自不同聚类的原始变量和对偶变量耦合在一起,这可能会使分析复杂化,但我们提供的条件与解耦子问题的量相关,每个解耦子问题都涉及仅一个聚类内条目的双随机投影。此外,在输入affinity的一些模型下,这允许我们表征具有假连接的输入亲和性将没有假连接并且在双重随机投影之后在每个簇内良好连接的条件。然后,我们专门研究子空间聚类数据模型,其中假设数据是从线性子空间的并集生成的,每个子空间定义一个聚类。对于这种设置,我们发展了一个连续问题,即在数据点数量变得非常大且均匀分布的极限中,然后是解耦定理的连续对应。这允许分析错误连接和投影affinity的连接性,这仅取决于子空间维度、每个子空间内的点的百分比以及子空间之间的角度。特别地,我们表明,如果子空间在角度上足够分离,或者具有足够低的维数,或者在混合权重方面很好地平衡,则在归一化后亲和矩阵中不会有错误连接。最后,我们进行了各种实验,这些实验说明了我们的理论发现,并证明了双重随机投影在不同环境中的效用。
2 双随机聚类
2.1 问题
考虑具有n个来自k个类别的数据点,类簇 l l l包含了 n l n_l nl个点,故 n = n 1 + ⋅ + n k n=n_1 + \cdot + n_k n=n1+⋅+nk。定义类簇 l l l的混合权重为 π l = n l n \pi_l=\frac{n_l}{n} πl=nnl。在给定对称且非负的affinity矩阵 K ∈ R n × n K\in\mathbb R^{n\times n} K∈Rn×n,其元素可以被看做点对之间的相似度。双随机聚类是两步走的方法。
第一步,将K的缩放版本投影到双随机矩阵集合上:

在某种距离
d
\mathfrak{d}
d概念下:
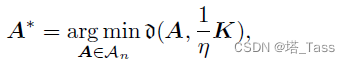
其中
η
>
0
\eta >0
η>0是缩放参数。
第二步,使用 A ∗ A^* A∗而非 K K K用于谱聚类。投影到 A n A_n An集合空间的一个直接优点是,不需要在Ratio Cut和NCut之间进行选择,因为两者在双随机affinity上是等价的。
作者注:两种cut将得到相同的图拉普拉斯: L = I − 1 n A ∗ L=I-\frac{1}{n}A^* L=I−n1A∗
距离
d
\mathfrak{d}
d的选择
经典的谱聚类方法对应于在不同距离下将给定的亲和度K投影到双随机矩阵A的集合上:Ratio Cut类似于
ℓ
1
ℓ_1
ℓ1度量下的投影,而NCut对应于在KL散度下的投影。一个有趣的也是自然的选择是使用
ℓ
2
ℓ_2
ℓ2范数作为距离。值得注意的是,
ℓ
2
ℓ_2
ℓ2度量在各种现实数据集上的子空间聚类中产生了最好的性能。这在很大程度上是由于经验观察到,这种投影通过控制输出affinity的稀疏性的参数
η
η
η,使得在消除错误连接和保持连通性之间取得了平衡。然而,这种稀疏性控制在使用
ℓ
1
ℓ_1
ℓ1范数投影时不存在,在使用 KL 散度进行投影时也不存在。
affinity连通性的重要性
请注意,没有错误连接不足以保证正确的聚类。一个类簇内的连接可能因为连通性不足不会形成连接子图,导致被过度分割。此外,谱聚类的稳定性与每个类簇是否足够好地连接有关。因此,最终聚类的稳定性得益于在每个聚类内尽可能连接的affinity。
本文重点研究了双随机在
ℓ
2
ℓ_2
ℓ2度量下的投影,我们称之为DS-D
(
K
,
η
)
(K,\eta)
(K,η),即:
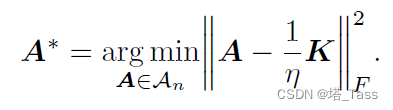
2.2 最优性分析
我们首先研究了DS-D
(
K
,
η
)
(K,\eta)
(K,η)的最优性条件。由于该问题是强凸的,标准的原对偶分析给出了全局最优性的以下充要条件:
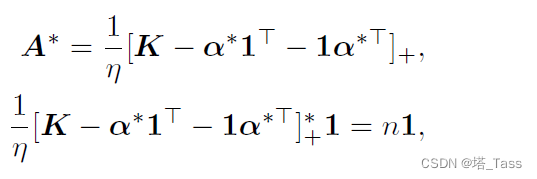
其中第一个公式中的
A
∗
A^*
A∗是唯一最优解,而
a
∗
∈
R
n
a^*\in \mathbb R^n
a∗∈Rn是满足第二个公式的对偶解。其中
[
⋅
]
+
∗
=
m
a
x
(
⋅
,
0
)
[\cdot]_+^*=\mathrm{max}(\cdot,0 )
[⋅]+∗=max(⋅,0)是元素级操作。
从解的形式来看,无错误连接性质相当于说:对于所有不同的 i , j i,j i,j簇,有 K i j ≤ α i ∗ + α j ∗ K_{ij}≤α^*_i+α^*_j Kij≤αi∗+αj∗。因此,我们希望找到 α ∗ α^* α∗的下界,以满足 A ∗ A^* A∗具有无错误连接性质的充分条件。由于 α ∗ α^* α∗的元素耦合,以有意义的方式直接限制 α ∗ α^* α∗ 是非常重要的。正如我们在下一个结果中所示,当且仅当DS-D ( K , η ) (K,\eta) (K,η)问题可以沿着affinity矩阵的类间部分解耦为一系列双随机投影问题时,才满足无错误连接性质。
不失一般性地,我们把affinity
K
K
K按照类簇的顺序排列,即:
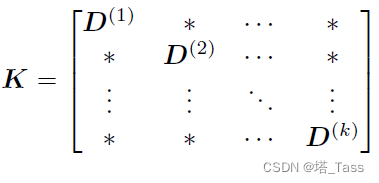
其中 D ( l ) ∈ R n l × n l D^{(l)}\in \mathbb R^{n_l\times n_l} D(l)∈Rnl×nl为类簇 l l l的类内affinity。利用 D ( l ) D^{(l)} D(l)我们有以下定理:
也就是说,连通性要求 D ( l ) D^{(l)} D(l)要构成连通子图(注意不是全部有非零值!);而无错误链接要求所有其它的 ∗ * ∗号部分全为0。
定理2.2:以下情况是等价的:
Statement 1: 对于每个类簇
l
l
l,存在DS-D
(
D
(
l
)
,
η
π
l
)
(D^{(l)},\frac{\eta}{\pi_l})
(D(l),πlη)的对偶解
α
(
1
)
∈
R
n
l
\alpha^{(1)}\in\mathbb R^{n_l}
α(1)∈Rnl,使得
α
i
∘
+
α
j
∘
≥
K
i
j
\alpha^\circ _i + \alpha^\circ _j \geq K_{ij}
αi∘+αj∘≥Kij对所有来自两个不同类簇的点
i
i
i和
j
j
j成立。其中,
α
i
∘
:
=
[
α
i
(
1
)
⊤
,
⋯
,
α
i
(
k
)
⊤
]
⊤
∈
R
n
\alpha^\circ_i :=[\alpha^{(1)\top}_i,\cdots , \alpha^{(k)\top}_i]^\top \in \mathbb R^n
αi∘:=[αi(1)⊤,⋯,αi(k)⊤]⊤∈Rn。
Statement 2: 双随机投影空间
A
∘
:
=
d
i
a
g
(
1
π
1
A
(
1
)
,
⋯
,
1
π
k
A
(
k
)
)
A^\circ :=\mathrm{diag}(\frac{1}{\pi_1}A^{(1)},\cdots , \frac{1}{\pi_k}A^{(k)})
A∘:=diag(π11A(1),⋯,πk1A(k))是DS-D
(
K
,
η
)
(K,\eta)
(K,η)的唯一最优解,其中对于每个类簇
l
l
l,
A
(
l
)
A^{(l)}
A(l)是DS-D
(
D
(
l
)
,
η
π
l
)
(D^{(l)},\frac{\eta}{\pi_l})
(D(l),πlη)的唯一最优解。
Statement 3: DS-D
(
K
,
η
)
(K,\eta)
(K,η)的唯一最优解不含有错误连接。
以上定理的证明见附录。这个定理意味着,如果对 K K K中的每个类内块 D ( l ) D^{(l)} D(l)求解了 D S − D DS-D DS−D子问题,那么整个 K K K矩阵的DS-D问题的解将没有错误连接,当且仅当该解可以通过将所有簇内解连接成块对角矩阵来形成。从这个结果中,我们可以给出affinity矩阵的几个简单性质的直接推论,这些性质足以保证无错误连接性质。
推论2.3:恒定类内连接
假设
K
K
K使得对于每个类簇
l
l
l有类内链接都有值
μ
l
\mu_l
μl,即,
D
(
l
)
=
μ
l
1
n
l
1
n
l
⊤
D^{(l)}=\mu_l 1_{n_l}1_{n_l}^\top
D(l)=μl1nl1nl⊤,那么DS-D
(
K
,
η
)
(K,\eta)
(K,η)的唯一最优解是不含有错误连接且在类内是全连接的,只要原始的
K
K
K中的任何类间(
p
≠
q
p\neq q
p=q)错误连接的值最大不超过
1
2
(
μ
p
+
μ
q
−
η
π
p
−
η
π
q
)
\frac{1}{2}(\mu_p +\mu_q - \frac{\eta}{\pi_p}-\frac{\eta}{\pi_q})
21(μp+μq−πpη−πqη)
证明:假设原始
K
K
K中的类间错误连接存在上界,我们首先证明定理2.2中的statement 1在此情况下成立。根据2.1节中所示的最优性条件,有
α
(
l
)
:
=
1
2
(
μ
l
−
η
π
l
)
1
n
l
\alpha^{(l)}:=\frac{1}{2}\left ( \mu_l - \frac{\eta}{\pi_l} \right ) 1_{n_l}
α(l):=21(μl−πlη)1nl和
A
(
l
)
:
=
π
l
η
[
D
(
l
)
−
α
(
l
)
1
n
l
⊤
−
1
n
l
α
(
l
)
⊤
]
A^{(l)}:=\frac{\pi_l}{\eta}[D^{(l)}-\alpha^{(l)}1^\top_{n_l} - 1_{n_l}\alpha^{(l)\top}]
A(l):=ηπl[D(l)−α(l)1nl⊤−1nlα(l)⊤]。事实上,
A
(
l
)
A^{(l)}
A(l)的行和采用以下形式:
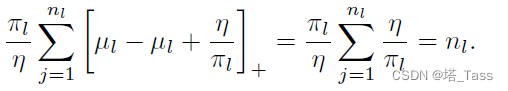
我们像statement 1中定义的那样,
α
i
∘
:
=
[
α
i
(
1
)
⊤
,
⋯
,
α
i
(
k
)
⊤
]
⊤
∈
R
n
\alpha^\circ_i :=[\alpha^{(1)\top}_i,\cdots , \alpha^{(k)\top}_i]^\top \in \mathbb R^n
αi∘:=[αi(1)⊤,⋯,αi(k)⊤]⊤∈Rn, 如果点
i
i
i来自
p
p
p类而点
j
j
j来自
q
q
q类,则根据以上求得的最优性对偶解,有
α
i
∘
+
α
j
∘
=
1
2
(
μ
p
+
μ
q
−
η
π
p
−
η
π
q
)
\alpha^\circ _i + \alpha^\circ _j = \frac{1}{2}(\mu_p +\mu_q - \frac{\eta}{\pi_p}-\frac{\eta}{\pi_q})
αi∘+αj∘=21(μp+μq−πpη−πqη)。于是既然有错误连接的值最大不超过
1
2
(
μ
p
+
μ
q
−
η
π
p
−
η
π
q
)
\frac{1}{2}(\mu_p +\mu_q - \frac{\eta}{\pi_p}-\frac{\eta}{\pi_q})
21(μp+μq−πpη−πqη)这一假定,于是statment 1就成立了。由等价的statement 2可得DS-D
(
K
,
η
)
(K,\eta)
(K,η)的最优解
A
∘
A^\circ
A∘在类内是全连接的。由等价的statment 3
A
∘
A^\circ
A∘没有错误连接。
推论2.4: 恒定最大类内内连接之和
假定
K
K
K使得对于所有类
l
l
l存在整数
σ
l
\sigma_l
σl得到
D
(
l
)
D^{(l)}
D(l)的
σ
l
\sigma_l
σl最近邻图
S
(
l
)
S^{(l)}
S(l)满足以下:
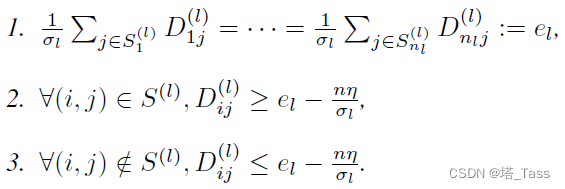
那么DS-D
(
K
,
η
)
(K,\eta)
(K,η)的最优解将没有错误连接且在类簇
l
l
l内沿着
σ
l
\sigma_l
σl最近邻图连通,只要所有
K
K
K中类间的连接值不超过
1
2
(
e
p
+
e
q
−
n
η
σ
p
−
n
η
σ
q
)
\frac{1}{2}(e_p + e_q - \frac{n\eta}{\sigma_p} - \frac{n\eta}{\sigma_q})
21(ep+eq−σpnη−σqnη)
上述推论表明,只要任意两个不同的类簇间的错误连接小于最大类内连接的均值,减去某种与参数 η \eta η成比例的gap,那么最优的双随机投影将不含有错误连接且类内连接良好。
接下来的推论表明了由DS-D ( K , η ) (K,\eta) (K,η)解得的双随机投影对任何形式为 v 1 ⊤ + 1 v ⊤ v 1^\top + 1v^\top v1⊤+1v⊤的低秩矩阵的扰动是不变的,其中 v ∈ R n v\in \mathbb R^n v∈Rn,如元素级的常数 c ∈ R c\in \mathbb R c∈R的扰动。因此,双随机矩阵能够排除 K K K中特定的加性噪音污染。
推论2.5
对于任何向量
v
∈
R
n
v\in \mathbb R^n
v∈Rn,那么DS-D
(
K
,
η
)
(K,\eta)
(K,η)和DS-D
(
K
+
1
v
⊤
+
v
1
⊤
,
η
)
(K+1v^\top +v1^\top,\eta)
(K+1v⊤+v1⊤,η)最优解是一致的。特别地,对每个元素加上某个常数c不会改变DS-D
(
K
+
c
1
1
⊤
)
(K+c11^\top)
(K+c11⊤)的解。
证明:对于任何
v
v
v和双随机投影
A
A
A,注意到:
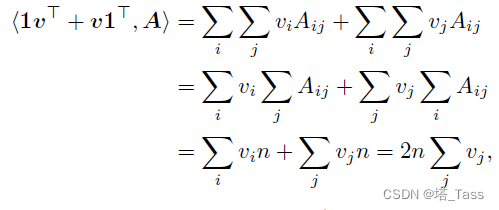
注意到由于双随机的性质,该内积化简成了一个与
A
A
A无关的常数。因此添加扰动后的最优解不变。第二部分的特例令
v
=
c
2
1
v=\frac{c}{2}1
v=2c1可证。
为什么内积与A无关可以得证?由DS-D的 ℓ 2 \ell_2 ℓ2范数定义,加入扰动的变化实际上就是A和扰动的内积部分,如果内积不包含A那么求解最优问题对A求导时该部分变为0,不影响A的最优解。
3. 双随机子空间聚类
我们在第2节对一般DS-D问题的进行了上述分析,我们现在考虑一个特定的数据模型来提供额外的分析。具体而言,我们将分析子空间聚类模型,它假设数据位于低维线性子空间的并集上。这是一个合理的假设,不过可能是在对数据进行预处理(如scattering变换)之后。最近使用双随机投影的工作已经在子空间聚类问题上取得了最先进的经验性能。
Notation
考虑分布在D维环境中的
k
k
k-子空间
{
S
l
}
l
=
1
k
\{\mathcal S_l\}_{l=1}^k
{Sl}l=1k,它们占用的低维维度为dim
S
l
:
=
d
l
<
D
\mathcal S_l := d_l < D
Sl:=dl<D。假设每个子空间
S
l
\mathcal S_l
Sl包含
n
l
n_l
nl个数据点,记为
X
(
l
)
X^{(l)}
X(l),这些数据点分布于单元球
S
D
−
1
\mathbb S^{D-1}
SD−1上。记
Φ
\Phi
Φ为子空间并集,
X
=
[
X
(
1
)
,
⋯
,
X
(
k
)
]
∈
R
D
×
n
X=[X^{(1)},\cdots , X^{(k)}]\in\mathbb R^{D\times n}
X=[X(1),⋯,X(k)]∈RD×n为数据集。
给定 X X X, 首先通过现有的子空间聚类方法计算affinity矩阵 K K K,然后求解DS-D ( K , η ) (K,η) (K,η)问题。对DS-D ( K , η ) (K,η) (K,η)的解执行谱聚类以获得最终的聚类结果。
3.1 连续问题的分析
由于从子空间模型的并集直接处理具有有限数据点的(离散)DS-D问题是非平凡的,因此我们考虑其连续对应问题:数据点的数量变得无限大且均匀分布。首先,我们定义了数据
X
X
X的离散测度:
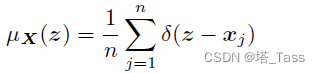
其中
δ
\delta
δ为单位球
S
D
−
1
\mathbb S^{D-1}
SD−1上的狄拉克函数使得对任何
f
:
S
D
−
1
→
R
f:\mathbb S^{D-1} \rightarrow \mathbb R
f:SD−1→R和
z
0
∈
S
D
−
1
z_0 \in \mathbb S^{D-1}
z0∈SD−1有:
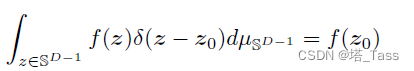
Dirac function: 积分为1的冲激函数
有了以上定义,我们可以把原始的离散目标看作:
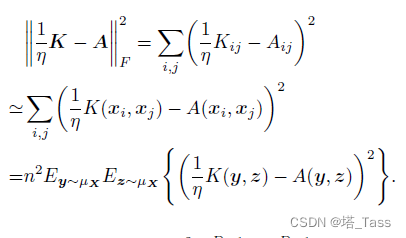
其中我们假设
K
∈
L
2
(
S
D
−
1
×
S
D
−
1
)
K\in L^2(\mathbb S^{D-1} \times \mathbb S^{D-1})
K∈L2(SD−1×SD−1)为核函数。类似地,双随机约束可以被写作:
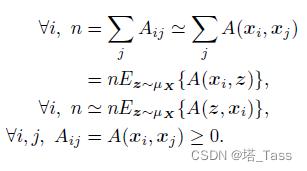
该离散度量可以按子空间分离为累和形式:
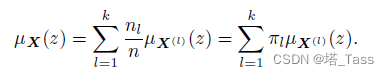
在连续情况下,将离散度量用它的连续近似替代:
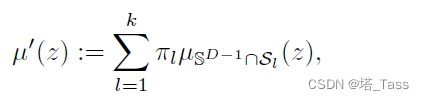
其中
μ
S
D
−
1
∩
S
l
\mu_{\mathbb S^{D-1}\cap \mathcal S_l}
μSD−1∩Sl是
S
D
−
1
∩
S
l
{\mathbb S^{D-1}\cap \mathcal S_l}
SD−1∩Sl上的均匀度量,有DS-D
(
K
,
η
)
(K,η)
(K,η)问题的连续版本:
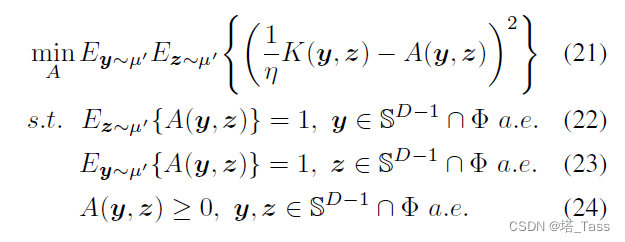
根据对二次正则化最优运输问题的分析, A ∗ ∈ L 2 ( S D − 1 × S D − 1 ) A^*\in L^2(\mathbb S^{D-1} \times \mathbb S^{D-1}) A∗∈L2(SD−1×SD−1)是问题的解当且仅当存在对偶函数 α ∗ ∈ L 2 ( S D − 1 ) \alpha^*\in L^2(\mathbb S^{D-1}) α∗∈L2(SD−1)使得:
Lorenz, D. A., Manns, P., and Meyer, C. Quadratically regularized optimal transport. Applied Mathematics & Optimization, 83(3):1919–1949, June 2021.
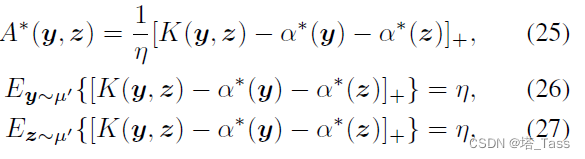
Remark:该连续问题是强凸的,因此存在唯一最优解。然而存在无数多个对偶解
α
∗
\alpha^*
α∗因为
[
⋅
]
+
[\cdot]_+
[⋅]+把负数的输入输出为0。
类似于离散问题的情况,满足无错误连接性质的解 A ∗ A^* A∗等于说,对于来自不同子空间的所有 y y y和 z z z, K ( y , z ) ≤ α ∗ ( y ) + α ∗ ( z ) K(y,z)≤α^*(y)+α^*(z) K(y,z)≤α∗(y)+α∗(z)几乎是肯定的。同样,我们可以将 α ∗ ( y ) α^*(y) α∗(y)从不同的子空间中分离为 y y y,以显示何时满足子空间保持性质的等价条件。
我们说该解是子空间保持等价于无错误连接
3.2 以Inner Product Kernel为例
为了展示双随机投影在子空间聚类问题中的作用,我们考虑原始输入 K K K采用最简单的内积核函数,即: K ( y z ) = ∣ ⟨ y , z ⟩ ∣ K(y_z)=|\langle y,z\rangle| K(yz)=∣⟨y,z⟩∣。我们做以下定义:
定义3.3:球形帽的平均高度
对于任何维度
d
d
d,定义:
ρ
d
(
α
)
=
∫
z
∈
S
d
−
1
[
∣
z
d
∣
−
2
α
]
+
d
μ
S
d
−
1
\rho_d(\alpha)=\int_{z\in\mathbb S^{d-1}}[|z_d|-2\alpha]_+\ d\mu_{\mathbb S^{d-1}}
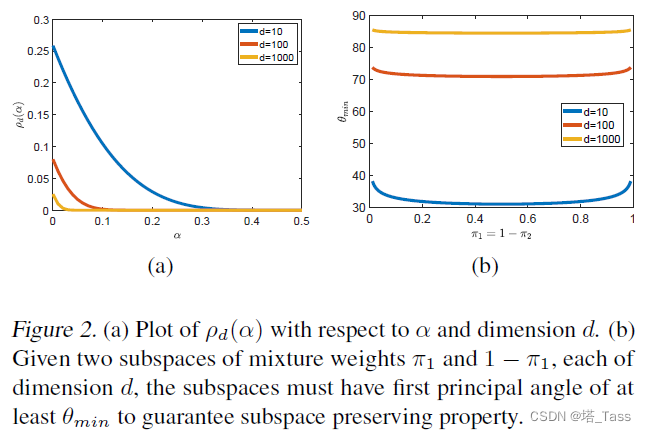
ρd(α)=∫z∈Sd−1[∣zd∣−2α]+ dμSd−1。如图(a)所示不同
α
\alpha
α和不同
d
d
d下
ρ
d
(
α
)
\rho_d(\alpha)
ρd(α)的变化。
定理3.4 子空间保持性质
令
K
K
K为内积核函数。如果对任何两个不同的子空间
S
p
\mathcal S_p
Sp和KaTeX parse error: Undefined control sequence: \mathcalS at position 1: \̲m̲a̲t̲h̲c̲a̲l̲S̲_q有:
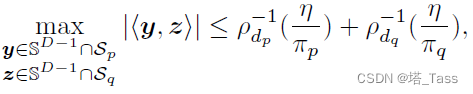
那么
A
∗
A^*
A∗是子空间保持的。注意到
ρ
d
−
1
(
η
π
)
\rho_d^{-1}(\frac{\eta}{\pi})
ρd−1(πη)随着维度的下降或者混合权重
π
\pi
π的增大而增大。对于给定的子空间和混合权重,子空间保持性质在
η
\eta
η足够小的时候成立,因为
lim
η
→
0
ρ
d
−
1
(
η
)
=
0.5
\lim_{\eta\rightarrow0}\rho_d^{-1}(\eta)=0.5
limη→0ρd−1(η)=0.5。如图(b)所示,子空间保持性质要求两个子空间之间的最小夹角必须足够大。当子空间越不均衡时(不同类簇的混合权重
π
\pi
π差距更大了)子空间需要更加分离。
定理3.5 连通性
令
K
K
K为内积核并假设
A
∗
A^*
A∗已满足子空间保持性质。对于任何子空间
S
l
\mathcal S_l
Sl,任意除了测度零的集合之外的两数据点
y
,
z
∈
S
l
∩
S
D
−
1
y,z\in \mathcal S_l\cap \mathbb S^{D-1}
y,z∈Sl∩SD−1在
A
∗
A^*
A∗中有一个非零连接,只要:
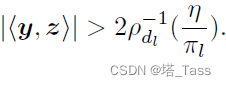
从上述两个结果中,我们可以保证双随机投影将达到所需的性质,即通过适当的参数η选择,
A
∗
A^*
A∗是子空间保持的和完全连通的。
4 实验
4.1 度量
- subspace preserving error (SPE) – 论文中为feature decection error(FDE)
- percent of false connections (PFC)
- number of non-zeros (NNZ) in A
- custering accuracy (ACC)
- normalized mutual information (NMI)
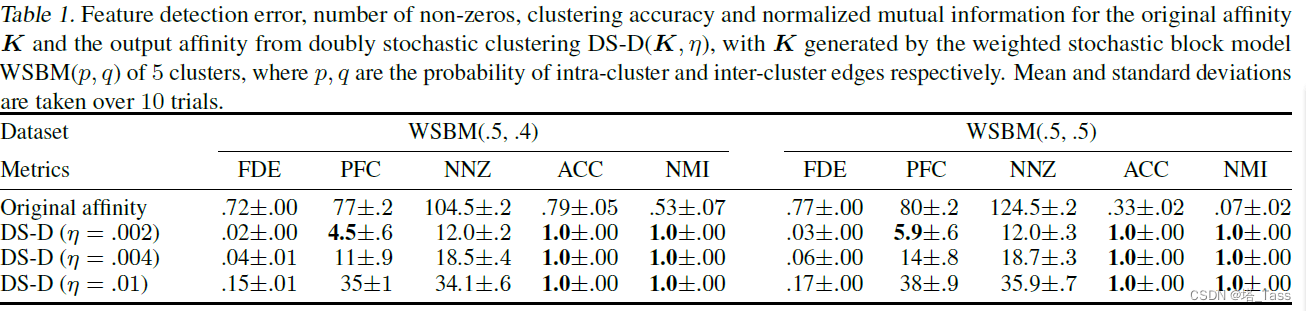
4.2 随机生成的块对角affinity

4.3 子空间聚类
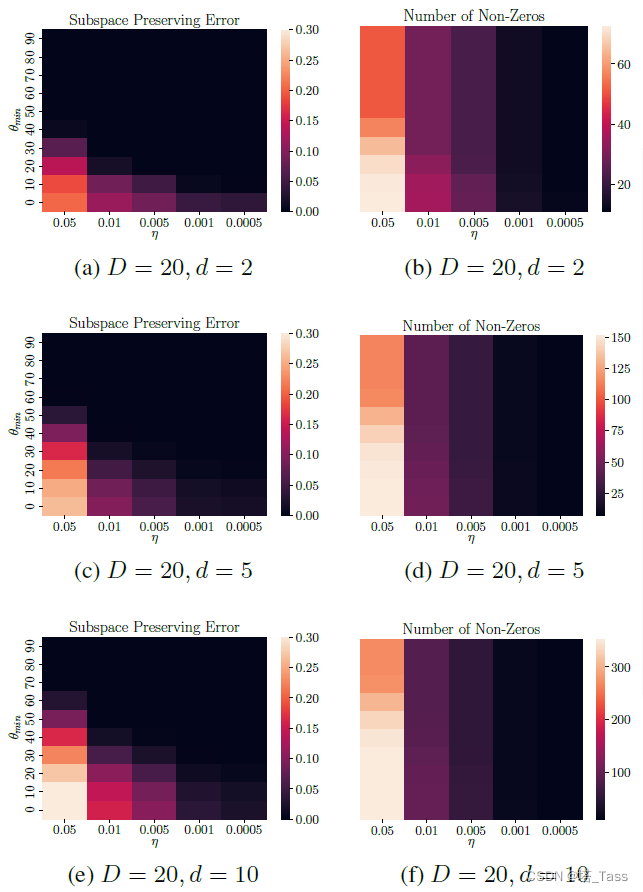
上图为双随机聚类DS-D
(
K
,
η
)
(K,\eta)
(K,η)输出的子空间保持误差和的非零个数,其中输入
K
K
K是来自
D
D
D维环境空间中维度为
d
d
d的两个子空间的内积核函数,每个子空间包含
n
=
50
⋅
d
n=50\cdot d
n=50⋅d个在单位范数上均匀分布的随机数据点。上图中随
η
\eta
η和最小子空间夹角
θ
m
i
n
\theta_{min}
θmin的变化规律证明了我们在定理中预测的子空间保持性质和连通性的几何条件。
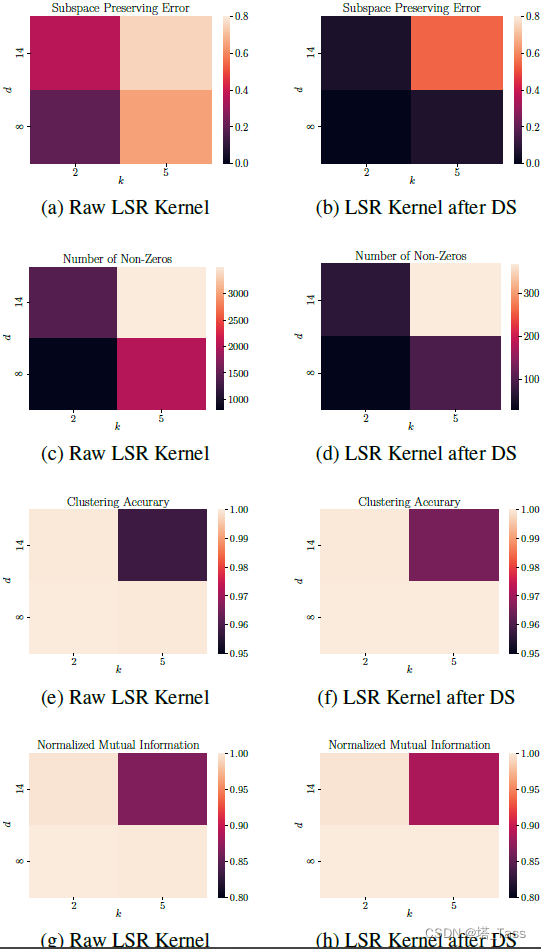
在应用双重随机投影之前和之后,Least Square Regression Kernel作为
K
K
K的子空间保持误差、非零数量、聚类准确率和归一化互信息,其中affnity来自
D
=
20
D=20
D=20中维度
d
d
d的
k
k
k个子空间的数据,每个子空间包含
n
=
50
⋅
d
n=50\cdot d
n=50⋅d个在单位范数上均匀分布的随机数据点。子空间和点都是随机均匀采样的。