引言
从本节开始,将介绍狄利克雷过程。
回顾:高斯混合模型
高斯混合模型(
Gaussian Mixture Model,GMM
\text{Gaussian Mixture Model,GMM}
Gaussian Mixture Model,GMM)是针对无监督学习中聚类任务的混合模型。
基于
N
N
N个样本的样本集合
X
=
{
x
(
i
)
}
i
=
1
N
\mathcal X = \{x^{(i)}\}_{i=1}^N
X={x(i)}i=1N,关于模型参数
θ
\theta
θ的学习过程,使用的底层逻辑是极大似然估计(
Maximum Likelihood Estimate,MLE
\text{Maximum Likelihood Estimate,MLE}
Maximum Likelihood Estimate,MLE):
arg
max
θ
[
log
P
(
X
)
]
=
arg
max
θ
[
∑
i
=
1
N
log
∑
k
=
1
K
α
k
⋅
N
(
x
(
i
)
∣
μ
k
,
Σ
k
)
]
\mathop{\arg\max}\limits_{\theta} \left[\log \mathcal P(\mathcal X)\right] = \mathop{\arg\max}\limits_{\theta} \left[\sum_{i=1}^N \log \sum_{k=1}^{\mathcal K} \alpha_{k} \cdot \mathcal N(x^{(i)} \mid \mu_k,\Sigma_{k})\right]
θargmax[logP(X)]=θargmax[i=1∑Nlogk=1∑Kαk⋅N(x(i)∣μk,Σk)]
它的模型参数
θ
\theta
θ具体包含三个部分:
当然,
α
\alpha
α一共包含
K
\mathcal K
K个离散信息,但如果求解出
α
1
,
⋯
,
α
K
−
1
\alpha_1,\cdots,\alpha_{\mathcal K-1}
α1,⋯,αK−1,那么最后一个
α
K
=
1
−
(
α
1
+
⋯
+
α
K
−
1
)
\alpha_{\mathcal K} = 1 - (\alpha_1 + \cdots + \alpha_{\mathcal K - 1})
αK=1−(α1+⋯+αK−1)即可。
θ
=
{
μ
1
,
⋯
,
μ
K
,
Σ
1
,
⋯
,
Σ
K
,
α
1
,
⋯
,
α
K
−
1
}
\theta = \{\mu_1,\cdots,\mu_{\mathcal K},\Sigma_1,\cdots,\Sigma_{\mathcal K},\alpha_1,\cdots,\alpha_{\mathcal K-1}\}
θ={μ1,⋯,μK,Σ1,⋯,ΣK,α1,⋯,αK−1}
关于高斯混合模型的概率图结构表示如下:
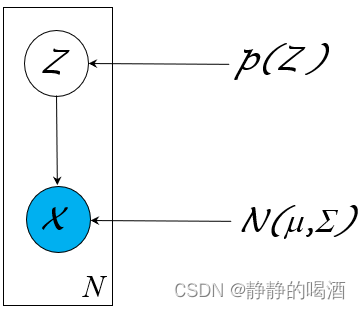
由于概率图结构简单,并且
Z
\mathcal Z
Z是一维的、离散型随机变量;
X
∣
Z
\mathcal X \mid \mathcal Z
X∣Z服从高斯分布,因而该模型是特殊的、直接使用
EM
\text{EM}
EM算法就可求解模型参数的模型结构。
狄利克雷过程——引出
关于某一个聚类任务,如果集合 X \mathcal X X在样本空间中的分布结构简单、易于观察聚类数量,我们可以轻易地定义聚类数量 K \mathcal K K的取值;
但如果处于某些原因,导致样本空间中的样本分布无法容易地观察出来。如:
这导致我们没有办法确定聚类数量
K
\mathcal K
K。一种想法是:如果将聚类数量
K
\mathcal K
K也作为模型参数
θ
\theta
θ的一部分:
θ
′
=
{
μ
1
,
⋯
,
μ
K
,
Σ
1
,
⋯
,
Σ
K
,
α
1
,
⋯
,
α
K
−
1
,
K
}
\theta' = \{\mu_1,\cdots,\mu_{\mathcal K},\Sigma_1,\cdots,\Sigma_{\mathcal K},\alpha_1,\cdots,\alpha_{\mathcal K-1},\mathcal K\}
θ′={μ1,⋯,μK,Σ1,⋯,ΣK,α1,⋯,αK−1,K}
从而使用极大似然估计去求解
K
\mathcal K
K。但真实情况下,这种方式可能是不可取的。我们首先观察对数似然函数
log
P
(
X
)
\log \mathcal P(\mathcal X)
logP(X):
log
P
(
X
)
=
∑
i
=
1
N
log
∑
k
=
1
K
α
k
⋅
N
(
x
(
i
)
∣
μ
k
,
Σ
k
)
\log \mathcal P(\mathcal X) = \sum_{i=1}^N \log \sum_{k=1}^{\mathcal K} \alpha_{k} \cdot \mathcal N(x^{(i)} \mid \mu_k,\Sigma_k)
logP(X)=i=1∑Nlogk=1∑Kαk⋅N(x(i)∣μk,Σk)
连加项中的核心构成是由聚类概率
α
k
\alpha_k
αk与对应高斯分布的概率密度函数
N
(
μ
k
,
Σ
k
)
\mathcal N(\mu_k,\Sigma_k)
N(μk,Σk)构成。可能出现如下情况:
当 K = N \mathcal K = N K=N时,即任意一个样本自身归为一类。那么某样本在基于该样本产生的高斯分布中,对应的概率密度函数结果一定是最大值。如果样本数量较少, α k ( k = 1 , 2 , ⋯ , K ) \alpha_{k}(k=1,2,\cdots,\mathcal K) αk(k=1,2,⋯,K)没有被划分的过于细碎,最终这种方法对应的 log P ( X ) \log \mathcal P(\mathcal X) logP(X)可能会脱颖而出。
这种做法所划分出来的聚类结果,对于聚类任务来说是没有意义的。
针对这种聚类模糊的样本分布,我们可以尝试:
-
针对每一个样本 x ( i ) ( i = 1 , 2 , ⋯ , N ) x^{(i)}(i=1,2,\cdots,N) x(i)(i=1,2,⋯,N)构建一个对应的参数 θ ( i ) ( i = 1 , 2 , ⋯ , N ) \theta^{(i)}(i=1,2,\cdots,N) θ(i)(i=1,2,⋯,N);
其中θ ( i ) ( i = 1 , 2 , ⋯ , N ) \theta^{(i)}(i=1,2,\cdots,N) θ(i)(i=1,2,⋯,N)的具体意义依然是描述对应样本x ( i ) ( i = 1 , 2 , ⋯ , N ) x^{(i)}(i=1,2,\cdots,N) x(i)(i=1,2,⋯,N)的聚类信息;只不过θ ( i ) \theta^{(i)} θ(i)仅仅对x ( i ) x^{(i)} x(i)一个样本负责。 -
此时,已经有了 N N N个参数 θ \theta θ,对于每一个参数 θ ( i ) \theta^{(i)} θ(i),它均会服从某个分布 H ( θ ) \mathcal H(\theta) H(θ):
θ ( i ) ∼ H ( θ ) i = 1 , 2 , ⋯ , N \theta^{(i)} \sim \mathcal H(\theta) \quad i=1,2,\cdots,N θ(i)∼H(θ)i=1,2,⋯,N
需要对分布 H ( θ ) \mathcal H(\theta) H(θ)进行限制,假设 H ( θ ) \mathcal H(\theta) H(θ)是一个连续分布( Continuous Distribution \text{Continuous Distribution} Continuous Distribution),那会出现什么样的情况?假设各样本之间独立同分布( Independent Identical Distribution,IID \text{Independent Identical Distribution,IID} Independent Identical Distribution,IID),并且样本之间不存在重复。对于数据集合中任意两个样本 x ( i ) , x ( j ) ∈ X x^{(i)},x^{(j)} \in \mathcal X x(i),x(j)∈X,其对应的 θ ( i ) , θ ( j ) \theta^{(i)},\theta^{(j)} θ(i),θ(j)不相同的概率无限接近于 0 0 0。这导致的直接后果是:任意两个样本对应的概率分布均不相同。
θ ( i ) , θ ( j ) ∼ H ( θ ) ⇒ P ( θ ( i ) = θ ( j ) ) = 0 \theta^{(i)},\theta^{(j)} \sim \mathcal H(\theta) \Rightarrow \mathcal P(\theta^{(i)} = \theta^{(j)}) = 0 θ(i),θ(j)∼H(θ)⇒P(θ(i)=θ(j))=0此时又回到了上面的问题:每个样本的分布均不相同,意味着 K = N \mathcal K = N K=N。这样的聚类结果自然没有意义。
-
但实际上,由于样本 x ( i ) x^{(i)} x(i)之间的差异性,对应参数 θ ( i ) \theta^{(i)} θ(i)之间同样存在差异。因而 H ( θ ) \mathcal H(\theta) H(θ)确实是一个关于 θ \theta θ的连续分布。但因为上面的问题,不能从 H ( θ ) \mathcal H(\theta) H(θ)中直接采样。因而需要找到一个和 H ( θ ) \mathcal H(\theta) H(θ)相似的离散分布。该离散分布记作 G \mathcal G G,具体表示如下:
G ∼ DP ( α , H ) \mathcal G \sim \text{DP}(\alpha,\mathcal H) G∼DP(α,H)
其中
DP
\text{DP}
DP是指狄利克雷过程(
Dirichlet Process,DP
\text{Dirichlet Process,DP}
Dirichlet Process,DP);
α
\alpha
α表示产生分布
G
\mathcal G
G离散型程度的标量(
Scalar
\text{Scalar}
Scalar)参数:
α
\alpha
α自身是一个大于
0
0
0的标量。
-
如果 α \alpha α的数值越大,通过狄利克雷过程 DP ( α , H ) \text{DP}(\alpha,\mathcal H) DP(α,H)产生的分布 G \mathcal G G越不离散。
一个分布越离散是指该分布对特征选择的种类越少。最离散的效果就是分布对某种类别选择的概率是1,没有其他选择。
相反,越不离散是指该分布对特征选择的种类很多,对每一个种类的选择均有相应的概率结果。如果 α \alpha α的取值是无穷大,那么该分布就变成了连续分布 H ( θ ) \mathcal H(\theta) H(θ)。 -
相反, α \alpha α的数值很小,那么产生的分布 G \mathcal G G会非常的离散。
举个例子。下图的蓝色点表示关于
H
(
θ
)
\mathcal H(\theta)
H(θ)的二维高斯分布:
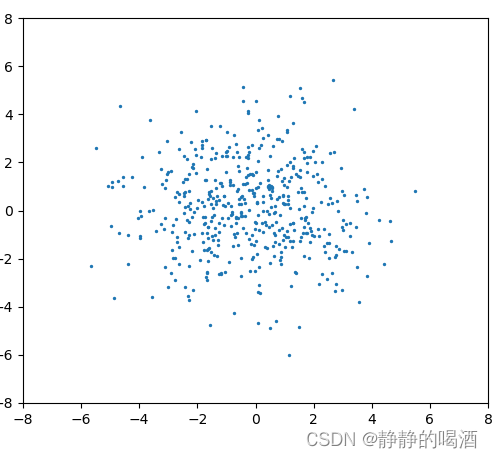
这明显是一个连续型分布。我们想通过狄利克雷过程
DP
(
α
,
H
)
\text{DP}(\alpha,\mathcal H)
DP(α,H)去构建一个离散分布
G
\mathcal G
G,使
G
\mathcal G
G能够近似分布
H
\mathcal H
H。
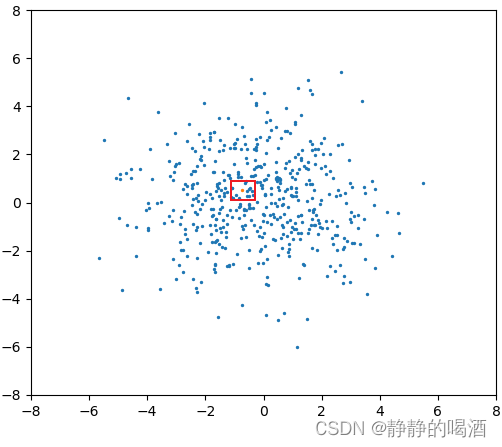
- 根据上面的描述,如果
α
\alpha
α取值为
0
0
0,产生
G
\mathcal G
G分布的样本点表示如下(橙色点):
此时属于‘最离散的状态’,无论怎样去随机采样,最终得到的只有一种选取结果,红色框标注。
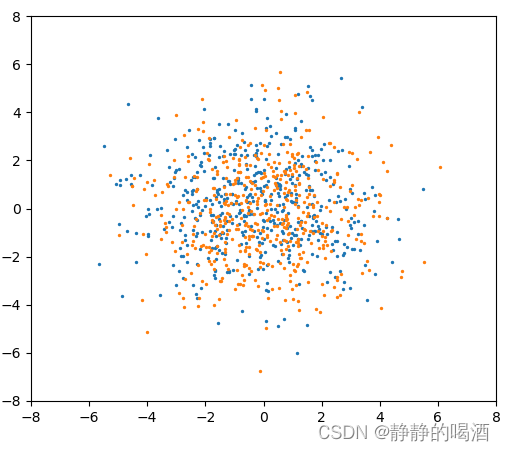
- 相反,如果
α
\alpha
α的取值足够高,对应产生
G
\mathcal G
G分布的样本点表示如下(依然是橙色点):
此时,它的离散分布状态足够多,每种状态都能分到对应的概率结果,当α ⇒ ∞ \alpha \Rightarrow \infty α⇒∞时,此时的离散分布G \mathcal G G等于连续分布H \mathcal H H。
当然,无论是上述哪种极端情况,都是不可取的:
- 如果样本分布过于离散,就如上述一个橙色样本表示整个概率分布一样,那么样本分布表达的准确性是较差的;
- 相反,如果样本更偏于连续,产生的分布可能会产生过拟合的现象,并且对于采样过程也存在较大的负担。
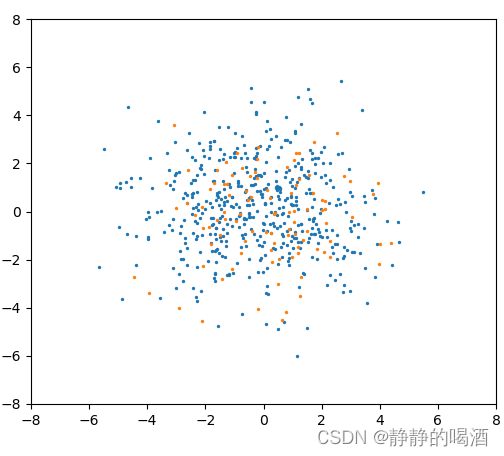
- 因而我们需要一个尽可能地将分布
H
\mathcal H
H的信息表示出来的离散分布(效果图):
相关参考:
徐亦达机器学习:Dirichlet Process Part 1